МОДЕЛЮВАННЯ ВОЛАТИЛЬНОСТІ ФОНДОВОГО РИНКУ ЗА ДОПОМОГОЮ ІНДЕКСУ ПФТС

Буртняк І.В.
д.е.н., професор
bvanya@meta.ua
Малицька Г.П.
к.фіз-мат.н., доцент
ДВНЗ Прикарпатський національний університет ім. В. Стефаника (Україна)

Ми досліджуємо залежність зміни волатильності індексу ПФТС на базі модифікованої моделі Блека-Шоулза, яку запропонували Гобсон і Роджерс [1].

Для проведення аналізу ми використали значення величини індексу ПФТС, за період з початку січня 2017 р. по кінець грудня 2019 р. Нехай \(P_t\) – значення індексу в момент часу \(t\), \(Z_t=ln(e^{-rt}P_t)\) – логарифмічно дисконтоване значення ціни індексу, \(S_{t}^{(m)}=\lambda \int_{0}^{\infty} e^{-\lambda u} (Z_t-Z_{t-u})^m du\) , де параметр \(\lambda\) описує вагу історичних спостережень. Величина індексу задовольняє стохастичне диференціальне рівняння \(dZ_t = \sigma (t, Z_t, S_t^{(1)}, \ldots, S_t^{(n)}) dB_t + \mu (t, Z_t, S_t^{(1)}, \ldots, S_t^{(n)}) dt\) [2]. Нехай \(e^{-rt}P_t\) буде \(\overline{P}\) – мартингал, який є розв’язком стохастичного рівняння \(d\overline{P} = \sigma \overline{P_t} d \overline{B_t}\) , де \(B_t\) – броунівський рух, за формулою Іто \(dZ_t = \sigma d\overline{B_t} - \frac{1}{2} \sigma^2 dt\).

Обчислимо значення функції \(S\)

\[ \overline{S_t} = \sum_{i=0}^M \frac{w_i}{W} (Z_t - Z_{t-i}), \tag{1} \]

де \(w_i = e^{-\lambda i \triangle t}\) – вагові коефіцієнти, а \(W\) – їхня сума. Як відповідну оцінку волатильності візьмемо \(\overline{\sigma_t} = \sqrt{k \sum_{i=1}^M \frac{w_i}{W} (Z_t - Z_{t-i} - \overline{\mu_t})^2}\) де \(\overline{\mu_t} = ln \frac{M - t}{t}\) – ваговий коефіцієнт, \(k = W^2 / \sum (\frac{W^2}{M} - w_i^2)\) , це коректувальний коефіцієнт для неупередженої оцінки \(\sigma^2\). Всі оцінки обчислені для щоденних даних, ми розглядаємо 122 операційних дні та маємо на увазі одиницю часу \(\triangle t = 1/122\).

Взявши \(M\) = 1224, обчислимо оцінку, засновану на 1224 історичних спостереженнях за кожним з операційних днів.

На рис. 1 наведено зв’язок між оцінкою (1) та волатильністю \(\overline{\sigma_t}\) обчисленої за допомогою частки квадратних тричленів \(\sigma(S) = \frac{1 + aS + bS^2}{c + dS + eS^2}\).

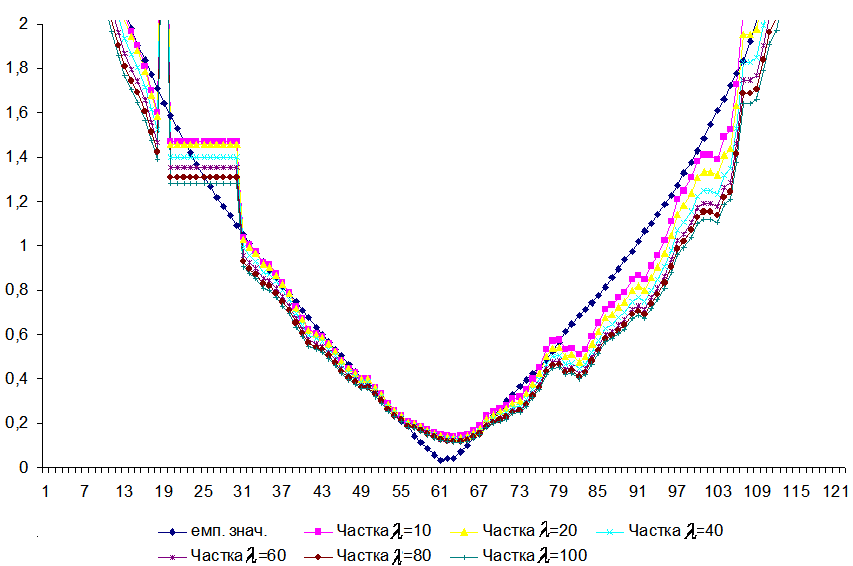
Рис. 1: Tренд волатильності, як частки двох многочленів.

Дослідження доводять, що найефективнішою специфікацією для функції волатильності є \(\sigma(S) = \frac{1 + aS + bS^2}{c + dS + eS^2}\), яка найкраще відображає відношення між відгалуженням і волатильністю, це значно зменшує зусилля, залучені на проблему оптимізації.

Дане дослідження забезпечує емпіричну очевидність на користь наших припущень і допомагає нам у виділенні відповідної функції волатильності

Шляхозалежна волатильність володіє минулою інформацією та дозволяє моделювати поведінку інвесторів в різних ринкових умовах, а також відображає позитивні або негативні тенденції використання фінансового інструменту. На відміну від стандартних локальних або стохастичних моделей волатильності, у випадку раптового падіння ринку, шляхозалежна модель волатильності може бути використана для автоматичного підвищення рівня волатильності з метою гармонізації динаміки фондового ринку.

ЛІТЕРАТУРА

1. Burtnyak, І.V., Malytska, A. Application of the spectral theory and perturbation theory to the study of Ornstein-Uhlenbesck processes. Carpathian Math. Publ. 2018, 10 (2), 273–287. doi:10.15330/cmp.10.2.273-287
2. Burtnyak I., Malytska A. (2019). Finding the derivative price using the Vasicek model with multidimensional stochastic volatility. Development Management, 17(4), 19-30.