МОДЕЛІ ОЦІНКИ ДВОБАР’ЄРНИХ ОПЦІОНІВ МЕТОДАМИ СПЕКТРАЛЬНОГО АНАЛІЗУ
Буртняк І.В.,
к.е.н., доцент кафедри економічної кібернетики
bvanya@meta.ua
Малицька Г.П.
к.фіз-мат.н., доцент кафедри математичного і функціонального аналізу
ДВНЗ Прикарпатський національний університет ім. В. Стефаника (Україна)
Розглянемо одновимірну дифузію з процесом Бесселя з дрифтом, який рівний нулю (є ряд процесів цього типу де дрифт не рівний нулю, але їх дослідження можна звести до процесів з нульовим дрифтом). Такі процеси мають застосування при розв’язуванні економічних задач на знаходження короткострокових відсоткових ставок, кредитних спредів та стохастичної волатильності деривативів [1].
Застосовано спектральний метод до ціноутворення похідних фінансових інструментів через представлення ціни похідного активу \(w(t,x)\), нейтрального до ризику за допомогою деякої функції майбутньої ціни основного активу X, тобто розглядається задача Штурма-Ліувілля.
\[\begin{equation} x^{2}w_{k}^{''} + xw_{k}^{'} + \left( {\lambda_{k}^{2}x}^{2} - p^{2} \right)w_{k} = 0, \tag{4} \end{equation}\]
\[\begin{equation} \left| w_{k} \right|_{x = 0} < + \infty, \tag{5} \end{equation}\]
\[\begin{equation} \alpha w_{k}^{'}\left( x_{0} \right) + \beta w_{k}\left( x_{0} \right) = 0. \tag{6} \end{equation}\]
Дана задача має єдиний розв’язок. Після певних перетворень нами отримано функціональні залежності які описують фінансові потоки на фондовому ринку:
\[ w\left( t,x \right) = \sum_{n = 0}^{\infty}{K{c_{n}e}^{- \left( \frac{\mu_{n}}{R - 1 - \ln\frac{R}{L}} \right)^{2}(T - t)}}\text{\ J}_{p}\left( \frac{\mu_{n}(x - K - \ln\frac{R}{L})}{R - L - \ln\frac{R}{L}} \right), \]
де \(\text{ J}_{p}\left( \frac{\mu_{n}(x - K - \ln\frac{R}{L})}{R - L -\ln\frac{R}{L}} \right)\) – функції Бесселя, \(\mu_{n}\) – корені рівняння (4), \(c_{n}\) – коефіцієнти розкладу в ряд, \(L < x < R,\ \ L,R\) – бар’єри, \(K\) – страйк (ціна виконання).
Для аналітичного задання ціни деривативів нами використано розклад функції Гріна по системах функцій Бесселя, для двохбар’єрної задачі, яка має вигляд
\[ G\left( t - \beta,x,\xi \right) = \sum_{n = 0}^{\infty}{\xi{\ J}_{p}\left( \frac{\mu_{n}\xi}{x_{0}} \right){\ J}_{p}\left( \frac{\mu_{n}x}{x_{0}} \right)e^{- \frac{\mu_{n}^{2}}{x_{0}}\left( t - \beta \right)}\left( \int_{0}^{x_{0}}{yJ_{p}^{2}\left( \frac{\mu_{n}y}{x_{0}} \right)\text{dy}} \right)^{- 1}}, \]
\[ w\left( t,x \right) = \int_{0}^{t}{G\left( t - \tau,x,\xi \right)f(\tau,\xi)d\xi}. \]
Використовуючи задачу (4) з крайовими умовами (5) і (6), нами охарактеризовані інтенсивності фінансових потоків.
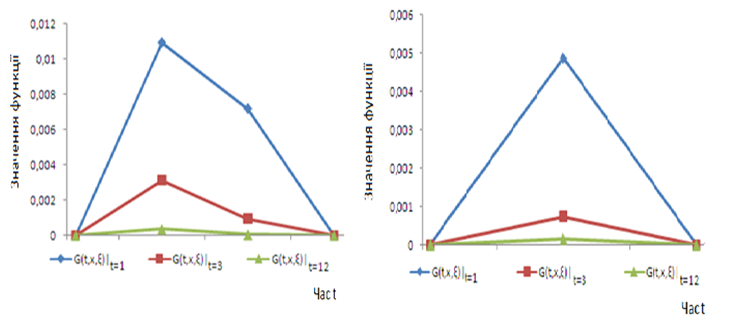
Рис. 6: Графік функції Гріна
Графік функції Гріна на рис. 6, як щільності розподілу процесів, які описують для двохбар’єрних опціонів величину ціни (зліва) та швидкість зміни ціни (справа) відповідно при \(L = 90,\ \ H = 120,\ \ \ \xi = 0,5\).
Поведінка похідних фінансових інструментів, зокрема, опціонів, яка описується стохастичними процесами, допускає явне представлення їх функцій щільності розподілів, що значно полегшує статистичну оцінку їхніх параметрів в процесі моніторингу ціноутворення деривативів та дослідження поведінки волатильності при аналізі дохідності та прийняття стратегічних управлінських рішень щодо здійснення операцій на фондовому ринку.
ЛІТЕРАТУРА
Burtnyak, І.V. , Malytska, A. Evaluating the financial flows of Bessel processes by using spectral analysis, Business Inform, 2017, 7, pp. 120–124.
Burtnyak, І.V., Malytska, A. The Evaluation of Derivatives of Double Barrier Options of the Bessel Processes by Methods of Spectral Analysis, Investment Management and Financial Innovations, 2017, Vol. 14, Issue 3, pp. 126–134.
Burtnyak, І.V. Malytska A. Application of the spectral theory and perturbation theory to the study of Ornstein-Uhlenbesck processes. Carpathian Math. Publ. 2018, 10 (2), 273–287.